5 多层感知机
沐神视频讲解:B站
教材:zh-v2.d2l.ai
5.1 感知机
给定输入x,权重w,和偏移b,感知机输出:
二分类:-1 或 1
- Vs. 回归输出实数
- Vs. Softmax回归输出概率
5.1.1 训练感知机
y与<w,x>(预测值)相乘
initialize w = 0 and b = 0
repeat
if then
end if
until all classified correctly
等价于使用批量大小为1的梯度下降,并使用如下的损失函数 x, w<w, x>
5.1.2 收敛定理
数据在半径r内
余量分类两类
(xw
对于||w||
感知机保证在步后收敛
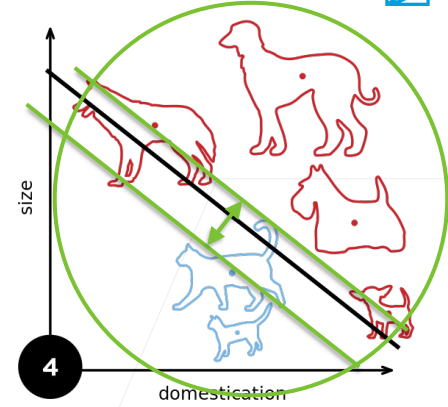
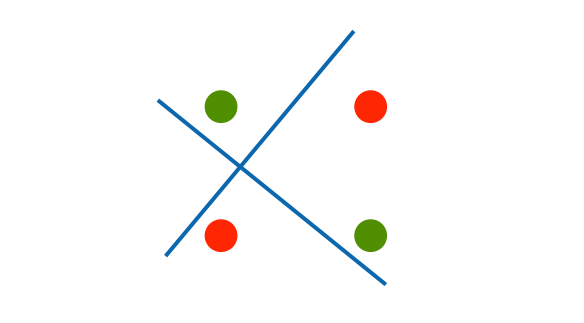
5.1.3 XOR问题
感知机不能拟合XOR问题,它只能产生线性分割面
5.1.4 总结
- 感知机是一个二分类模型,是最早的AI模型之一
- 它的求解算法等价于使用batch size = 1的梯度下降
- 它不能拟合XOR函数,导致的第一次AI寒冬
5.2 多层感知机
多层感知机(multilayer perceptron)使用隐藏层和激活函数来得到非线性模型
5.2.1 学习XOR
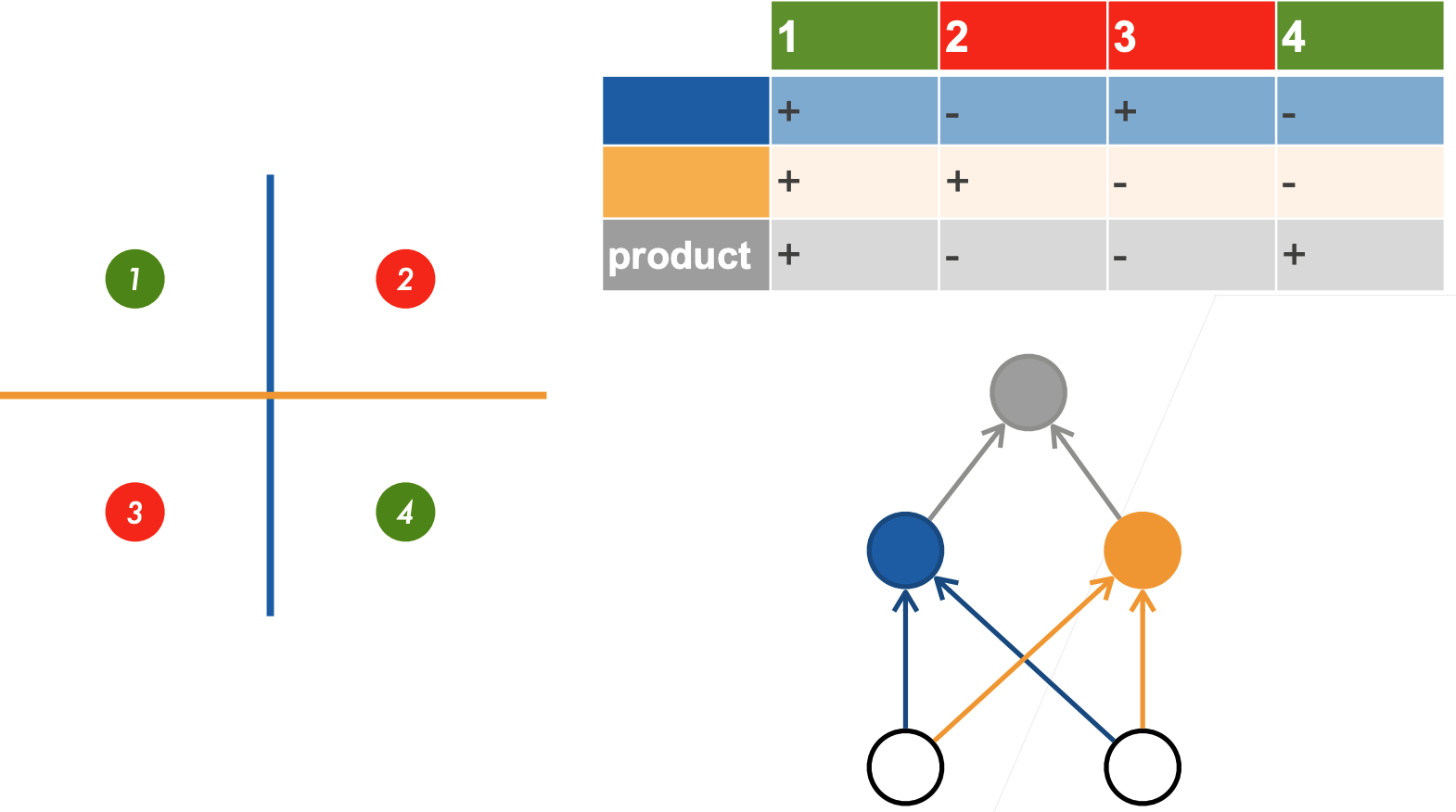
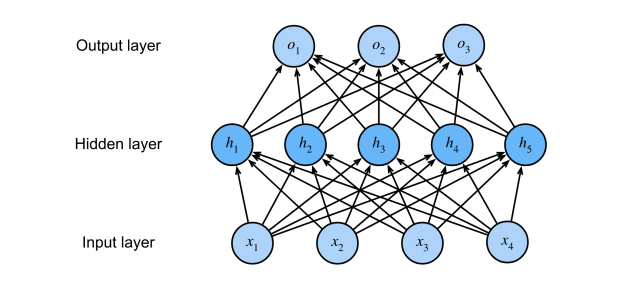
5.2.2 单分类——单隐藏层
隐藏层大小是超参数
输入
隐藏层
输出层
是按元素的
激活函数(activation function),为什么需要非线性激活函数?如果没有非线性的话,输出就是无限的线性函数套娃
5.2.3 激活函数
5.2.3.1 ReLU激活函数
ReLU: 修正线性单元(rectified linear unit)
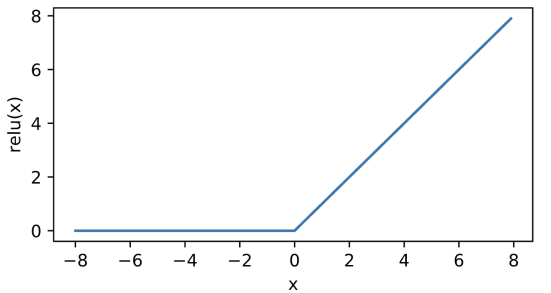
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。 注意,当输入值精确等于0时,ReLU函数不可导。 在此时,我们默认使用左侧的导数,即当输入为0时导数为0。 我们可以忽略这种情况,因为输入可能永远都不会是0。 这里引用一句古老的谚语,“如果微妙的边界条件很重要,我们很可能是在研究数学而非工程”, 这个观点正好适用于这里
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。 这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)
5.2.3.2 Sigmoid激活函数
sigmoid通常称为挤压函数(squashing function)将输入投影到(0, 1),是一个软的
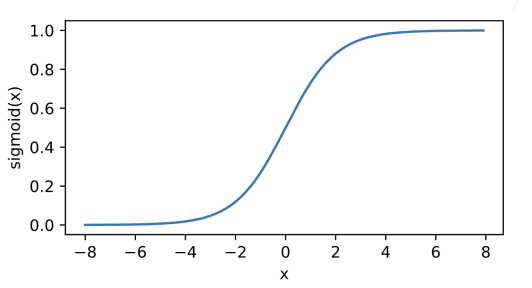
当我们想要将输出视作二元分类问题的概率时, sigmoid仍然被广泛用作输出单元上的激活函数 (sigmoid可以视为softmax的特例)。 然而,sigmoid在隐藏层中已经较少使用, 它在大部分时候被更简单、更容易训练的ReLU所取代
5.2.3.3 Tanh激活函数
将输入投影到(-1, 1)
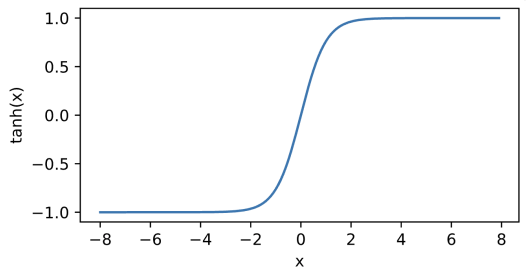
注意,当输入在0附近时,tanh函数接近线性变换。 函数的形状类似于sigmoid函数, 不同的是tanh函数关于坐标系原点中心对称
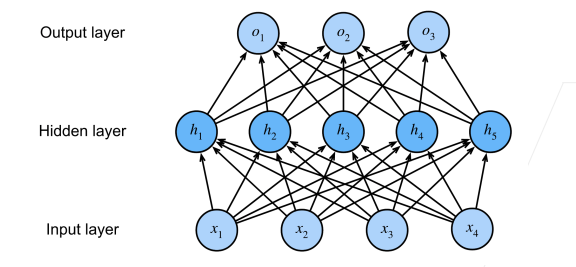
5.2.4 多类分类——单隐藏层
输入
隐藏层
输出层
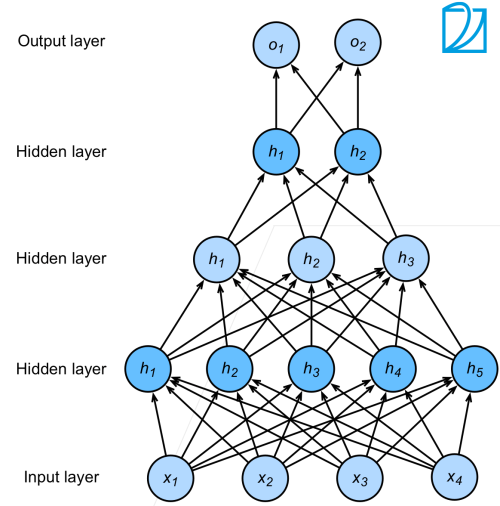
5.2.5 多隐藏层
超参数:隐藏层数、每层隐藏层的大小
5.3 多层感知机的从零实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 5, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
实现ReLU激活函数
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
实现模型
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X @ W1 + b1)
return (H @ W2 + b2)
loss = nn.CrossEntropyLoss(reduction='none')
多层感知机的训练过程与softmax回归的训练过程完全相同
num_epochs, lr = 5, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
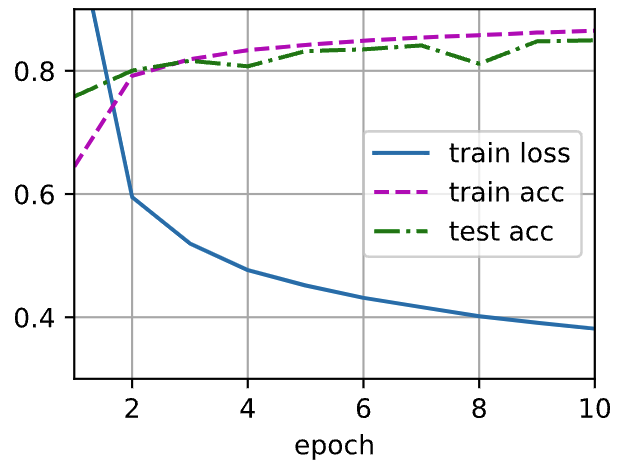
Output
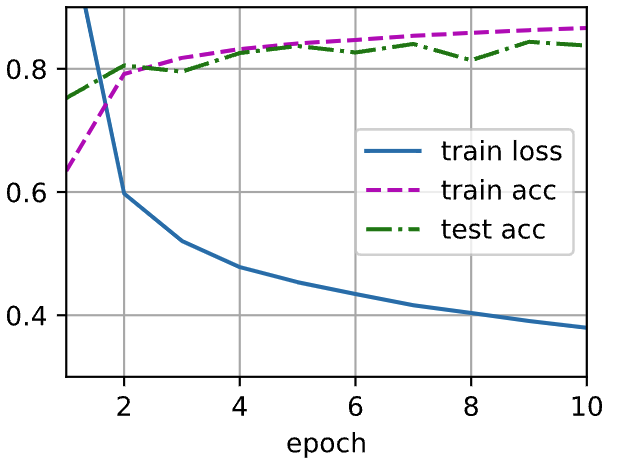
在一些测试数据上应用这个模型
d2l.predict_ch3(net, test_iter)
Output

5.4 多层感知机的简洁实现
高级API
import torch
from torch import nn
from d2l import torch as d2l
隐藏层包含256个隐藏单元,并使用了ReLU激活函数
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 5))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
训练过程
batch_size, lr, num_epochs = 256, 0.1, 5
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
Output